
2022.06.25
프로그래머스 '소수 만들기' 문제 피드백
1번째 시도: 성공
def solution(nums):
nums_sum = []
for i in range(len(nums) - 2):
for j in range(i + 1, len(nums) - 1):
for k in range(j + 1, len(nums)):
nums_sum.append(nums[i]+nums[j]+nums[k])
answer = 0
for i in nums_sum:
check = 0
for j in range(2, i//2 + 1):
if i % j == 0:
check = 1
break
if check == 0:
answer += 1
return answer
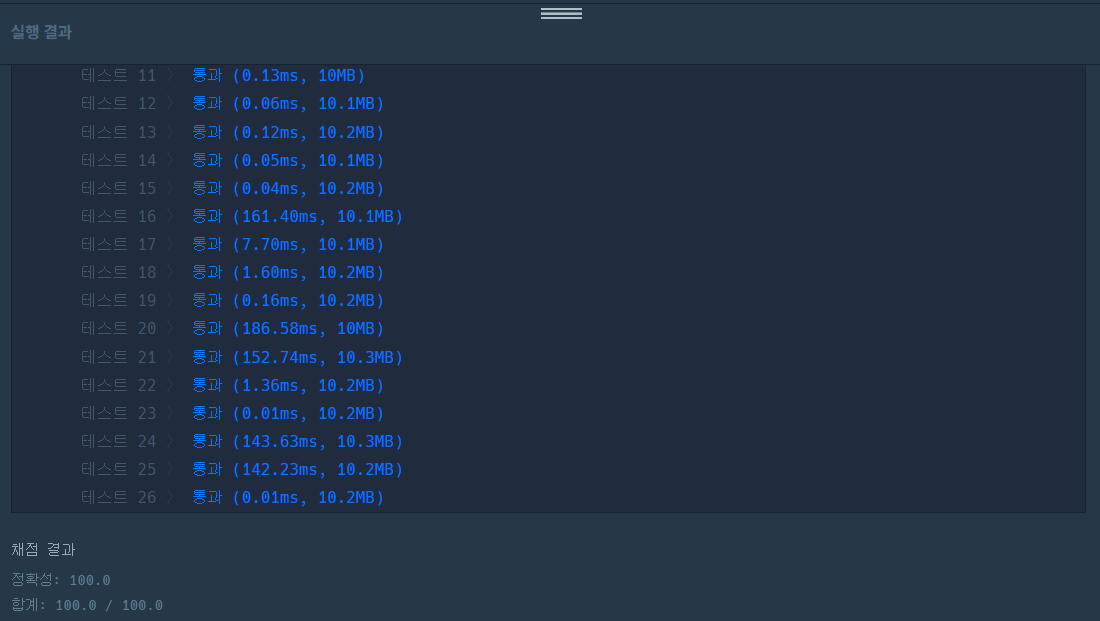
성공은 했는데 실행 시간이 너무 길다.
모범 답안 (1)
from itertools import combinations
def solution(nums):
answer = 0
for i in combinations(nums, 3):
nums_sum = sum(i)
for j in range(2, int(nums_sum**0.5)+1):
if nums_sum % j == 0:
break
else:
answer += 1
return answer
'itertools' library의 'combinations' function에 대해 알게 되었다.
- from itertools import combinations : 'combinations' function을 쓰려면 'itertools' library를 import 해야 함.
- combinations(nums, 3) : list 'nums'의 원소들 중 3개를 조합할 수 있는 모든 경우를 만듦
- int(nums_sum**0.5) + 1 : 소수인지를 판별하기 위해 2부터 시작해 나머지가 0이 되는 수가 있는지를 확인할 때, 2부터 그 수에 root(√) 씌운 수까지만 구하면 됨.

모범 답안 (2)
def sieve(n):
# 에라토스테네스의 체
if n < 2: return []
s = [0, 0] + [1] * (n - 1) #[0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
for i in range(2, int(n**.5)+1):
if s[i]:
s[i*2::i] = [0] * ((n - i)//i)
return [i for i, v in enumerate(s) if v]
def solution(nums):
primes = sieve(3000)
count = 0
for i in range(len(nums)-2):
for j in range(i+1, len(nums)-1):
for k in range(j+1, len(nums)):
if (nums[i] + nums[j] + nums[k]) in primes:
count += 1
return count
'에라토스테네스의 체'라는 방법으로 3부터 원하는 수 사이에 있는 모든 소수를 구할 수 있다.

그런데 이 방법을 이용한 실행 속도가 더 빠르지는 않았다.
'에라토스테네스의 체'를 이용하여 소수 구하기
def solution(n):
if n < 2:
return []
s = [0, 0] + [1] * (n-1)
for i in range(2, int(n**0.5)+1):
if s[i]:
s[i*2::i] = [0] * ((n - i) // i)
return s
'에라토스테네스의 체'를 이용하여 소수만 구한다.
return한 list s에서 값이 1인 index가 모두 소수이다.
(ex. [0, 0, 1] => 값이 1인 index는 2이므로, 2는 소수임)
'코딩테스트' 카테고리의 다른 글
| [코딩테스트, Python] 프로그래머스 Lv.1 쉬운 문제들 피드백 모음 (2) (0) | 2022.06.27 |
|---|---|
| [코딩테스트, Python] 프로그래머스 Lv.1 쉬운 문제들 피드백 모음 (1) (0) | 2022.06.26 |
| [코딩테스트, Python] 프로그래머스 '완주하지 못한 선수' 문제 피드백 (Feat. Hash Table) (0) | 2022.06.24 |
| [코딩테스트, Python] 프로그래머스 '신규 아이디 추천' 문제 피드백 (0) | 2022.06.24 |
| [코딩테스트, Python] 프로그래머스 '신고 결과 받기' 문제 피드백 (0) | 2022.06.23 |